More mathematics
Typesetting mathematics is a work of art. LaTeX knows a lot of the basics (more than any other), but you often have to fiddle to get best results---but then the onus is on us to know what is 'best'. Look at how to produce the mathematics shown in Src/maths.pdf
- include mathematics inline, with the \( ... \) environment, or displayed using either the \[ ... \] or equation environments;
- set sub- and super-scripts;
- use the \frac command to typeset fractions; and
- that many commands type mathematical symbols such as the Greek alphabet.
Thanks to MathJax for typesetting the following interleaved LaTeX fragments.
AMS-LaTeX
The American Mathematical Society has enormously extended the mathematical environments, commands, fonts and symbols in LaTeX. Get into the habit of accessing part of their extensions by putting \usepackage{amsmath} into the preamble. Investigate other extensions if you can spare the time.
Often useful are the American Mathematical Society's symbols: include with \usepackage{amssymb} in the preamble (download a list of the symbols). I strongly recommend you stay within the symbols provided by standard LaTeX and amssymb (listed in the first 32 pages of this summary by Emre Sremutlu).
For curvaceous capital letters in maths, do not use the font \mathscr as readers cannot differentiate between many of the characters, instead use \mathcal.
For procrastinators: interestingly, sketch the symbol you are looking for into the Detexify web server and it will list LaTeX possibilities. But beware, although great fun it is rarely useful to employ symbols from the 14,283 (Jan 2017) listed in The Comprehensive LaTeX Symbol List.
Theorems et al.
Repeating the end of the section on Environments, LaTeX does not by default provide an environment for theorems. Instead LaTeX provides an environment for you to create theorem-like environments (extended by the American Mathematical Society). I recommend you include the following in your preambles:
\usepackage{amsthm} % optional
... cleveref ...
\newtheorem{theorem}{Theorem}
\newtheorem{corollary}[theorem]{Corollary}
\newtheorem{lemma}[theorem]{Lemma}
\newtheorem{definition}[theorem]{Definition}
Thereafter, as seen in Section 1 of Src/maths.tex, you use the following environments as appropriate:
\begin{theorem}...\end{theorem}
\begin{corollary}...\end{corollary}
\begin{lemma}...\end{lemma}
\begin{definition}...\end{definition}
\begin{proof}...\end{proof}
The last proof environment is from the amsthm package.
Label and cross-reference these as usual.
Such environments obtained from \newtheorem may also have an optional argument to provide a name to the 'theorem'. For example,
\begin{definition}[right-angled triangles]...\end{definition}
Src/maths.tex also shows the extarticle class allows you to get larger fonts, e.g., for displays: 14pt, 17pt and 20pt.
Accents
When we want a distinct quantity that has a close relation to something else, often use a mathematical accent. Common mathematical accents over a single character, say a, are:
- \bar a to put an overbar over a;
- \tilde a to put '~' over a;
- \hat a to put '^' over a;
- \dot a to put a single dot over a;
- \ddot a to put a double dot over a; and
- \vec a to put a little arrow over a.
If necessary, accents may be stacked on top of each other. See Section 2 in Src/maths.tex.
| Mathematical accents are performed by a short command with one argument, such as \[ \tilde f(\omega)=\frac{1}{2\pi} \int_{-\infty}^\infty f(x)e^{-i\omega x}\,dx\,, \] or \[ \dot{\vec \omega}=\vec r\times\vec I\,. \] |
Mathematical accents are performed by a
short command with one argument, such as
\[
\tilde f(\omega)=\frac{1}{2\pi}
\int_{-\infty}^\infty f(x)
e^{-i\omega x}\,dx\,,
\]
or
\[
\dot{\vec \omega}=\vec r\times\vec I\,.
\]
|
Relations
LaTeX knows to typeset extra space around relations =, \approx, and
- inequalities < , > , \leq , \geq
- very much so \ll , \gg
- set relations \in , \subset
Delimiters
Common delimiters such as
- parentheses (...)
- brackets [...]
- braces \{...\}
- angle brackets \langle...\rangle (do not use the relations < and > for this purpose)
- bars |...| or \|...\|
| See how the delimiters are of reasonable size in these examples \[ \left(a+b\right)\left[1-\frac{b}{a+b} \right]=a\,, \] \[ \sqrt{|xy|}\leq\left|\frac{x+y}{2} \right|, \] even when there is no matching delimiter \[ \int_a^bu\frac{d^2v}{dx^2}\,dx =\left.u\frac{dv}{dx}\right|_a^b -\int_a^b\frac{du}{dx}\frac{dv}{dx} \,dx\,. \] |
See how the delimiters are of reasonable
size in these examples
\[
\left(a+b\right)\left[1-\frac{b}{a+b}
\right]=a\,,
\]
\[
\sqrt{|xy|}\leq\left|\frac{x+y}{2}
\right|,
\]
even when there is no matching delimiter
\[
\int_a^bu\frac{d^2v}{dx^2}\,dx
=\left.u\frac{dv}{dx}\right|_a^b
-\int_a^b\frac{du}{dx}\frac{dv}{dx}
\,dx\,.
\]
|
Note that \left and \right must be used in pairs so that LaTeX can determine the size of the intervening mathematics. If the matching delimiter is not to appear for any reason, such as splitting a sub-expression over two lines or for an evaluation bar, then use \left. or \right. to mark that boundary of the delimiter for LaTeX.
Spacing
In the previous examples I used \,, and \,. to punctuate at the end of the equations. Both in and out of maths, LaTeX provides spacing commands. The two necessary ones are the following:
- \, to typeset a thin space;
- \quad to typeset a 'quad' space (1em).
Use these to space the mathematics where needed.
For example, see Src/maths.tex, section 4,
- use \, to separate
- the infinitesimal from the integrand in integrals,
- punctuation from mathematics (when necessary),
- a number from its abbreviated physical units;
- use \quad to separate two or more equations or text on the one line.
| Differentials often need a bit of help with their spacing as in \[ \iint xy^2\,dx\,dy =\frac{1}{6}x^2y^3, \] whereas vector problems often lead to statements such as \[ u=\frac{-y}{x^2+y^2}\,,\quad v=\frac{x}{x^2+y^2}\,, \quad \text{and}\quad w=0\,. \] |
Differentials often need a bit of help
with their spacing as in
\[
\iint xy^2\,dx\,dy
=\frac{1}{6}x^2y^3,
\]
whereas vector problems often lead to
statements such as
\[
u=\frac{-y}{x^2+y^2}\,,\quad
v=\frac{x}{x^2+y^2}\,, \quad
\text{and}\quad w=0\,.
\]
|
Remember to use amsmath \iint and \iiint for multiple integrals as otherwise the spacing is awful. Use the amsmath \text{...} command to include a few words of ordinary text within mathematics.
Punctuation? The display or not of mathematics is irrelevant: punctuate a sentence as if the mathematical statements, phrases, and symbols are an integral part of the sentence.
When mathematics is inline (as opposed to displayed), then the sentence punctuation should be outside the mathematics environment (as otherwise the spacing is wrong).
In particular, avoid the odious proliferation of bad colons: for example avoid "Newton's second law is: \(F=ma\)." The rule for colons is that the two parts of the sentence on either side of a colon must make complete statements.
Occasionally one gets very bad line breaks when using a list in mathematics such as listing the first twelve primes \(2,3,5,7,11,13,17,19,23,29,31,37\). In such cases, you may include \mathcode`\,="213B inside the inline maths environment so that the list breaks. Be discerning.
Functions
LaTeX knows how to typeset a lot of mathematical functions.
- Trigonometric and other elementary functions are defined by the obvious corresponding command name. For example, \sin x or \exp(i\theta).
- Subscripts on more complicated functions, such as \lim_{..} and \max_{...} are appropriately placed under the function name.
- And the same goes for both sub- and super-scripts on large operators such as \sum, \prod and \bigcup.
See Section 5 in Src/maths.tex. Typeset all multicharacter mathematical names in upright roman: when a command is not available, use amsmath \operatorname{...} as in the Reynolds number \operatorname{Re}.
| Elementary functions are typeset properly, even to the extent of providing a thin space if followed by a single letter argument: \[ \exp(i\theta)=\cos\theta +i\sin\theta\,,\quad \sinh(\log x)=\frac{1}{2} \left( x-\frac{1}{x} \right). \] With sub- and super-scripts placed properly on more complicated functions, \[ \lim_{q\to\infty}\|f(x)\|_q =\max_{x}|f(x)|, \] and large operators, such as integrals and \[\begin{aligned} e^x &= \sum_{n=0}^\infty \frac{x^n}{n!} \quad\text{where }n!=\prod_{i=1}^n i\,, \\ \overline{U_\alpha} & = \bigcap_\alpha U_\alpha\,. \end{aligned}\] Here the overline denotes an operation (the intersection), as distinct from an accent which would be \bar. In inline mathematics the scripts are correctly placed to the side in order to conserve vertical space, as in \(1/(1-x)=\sum_{n=0}^\infty x^n.\) |
Elementary functions are typeset
properly, even to the extent of
providing a thin space if followed by a
single letter argument:
\[
\exp(i\theta)=\cos\theta +i\sin\theta\,,\quad
\sinh(\log x)=\frac{1}{2}
\left( x-\frac{1}{x} \right).
\]
With sub- and super-scripts placed
properly on more complicated functions,
\[
\lim_{q\to\infty}\|f(x)\|_q
=\max_{x}|f(x)|,
\]
and large operators, such as integrals and
\begin{align*}
e^x &= \sum_{n=0}^\infty \frac{x^n}{n!}
\quad\text{where }n!=\prod_{i=1}^n i\,, \\
\overline{U_\alpha}
& = \bigcap_\alpha U_\alpha\,.
\end{align*}
In inline mathematics the scripts are
correctly placed to the side in order to
conserve vertical space, as in
\(
1/(1-x)=\sum_{n=0}^\infty x^n.
\)
|
Command definitions
Recall that LaTeX provides a facility for you to define your very own commands. Since LaTeX does not have a predefined Airy function we would define our own:
\newcommand{\Ai}{\operatorname{Ai}}
and then use the command \Ai wherever needed.
| The Airy function, \(\newcommand{\Ai}{\operatorname{Ai}}\Ai(x)\), may be incorrectly defined as this integral \[ \Ai x=\int\exp(s^3+isx)\,ds\,. \] | The Airy function, $\Ai(x)$, may be incorrectly defined as this integral \[ \Ai x=\int\exp(s^3+isx)\,ds\,. \] |
Wherever you need a two (or three) letter mathematical constant (or function) such as Reynolds number Re, Prandtl number Pr, Peclet number Pe, etc, then you must use \operatorname{Re} and the like---most easily via a \newcommand.
More useful commands involve arguments; I give three of my favourites. The first two, with two arguments, define partial derivative commands
\newcommand{\D}[2]{\frac{\partial #2}{\partial #1}}
\newcommand{\DD}[2]{\frac{\partial^2 #2}{\partial #1^2}}
\renewcommand{\vec}[1]{\boldsymbol{#1}}
and the last, with one argument, redefines the \vec command to denote vectors by boldface characters (rather than have an arrow accent). Within a definition, #n denotes a placeholder for the nth supplied argument. See these in use in Section 6 of Src/maths.tex.
| This vector identity serves nicely to illustrate two of the new commands: \[ \newcommand{\D}[2]{\frac{\partial #2}{\partial #1}} \renewcommand{\vec}[1]{\mathbf{#1}} \vec\nabla\times\vec q =\vec i\left(\D yw-\D zv\right) +\vec j\left(\D zu-\D xw\right) +\vec k\left(\D xv-\D yu\right). \] | This vector identity serves nicely to illustrate two of the new commands: \[ \vec\nabla\times\vec q =\vec i\left(\D yw-\D zv\right) +\vec j\left(\D zu-\D xw\right) +\vec k\left(\D xv-\D yu\right). \] |
One can use commands at a higher level of abstraction: the following creates a command that defines commands. Here \Bb empowers us to consistently define commands such as \CC, \NN and \RR to consistently generate \(\mathbb C\), \(\mathbb N\) and\(~\mathbb R\).
\newcommand{\Bb}[1]{%
\expandafter\def\csname#1#1\endcsname%
{\ensuremath{\mathbb #1}}}
\Bb C\Bb N\Bb R
Arrays
Frequently we need to set mathematics in a tabular format.
The usual reason is to typeset a matrix using an amsmath matrix environment such as
\begin{bmatrix}
... & ... & ... & ... \\
... & ... & ... & ... \\
... & ... & ... & ...
\end{bmatrix}
for a bracketed matrix of three rows and four columns, see Src/maths.tex, Section 7. Use environments matrix for an array without brackets, and pmatrix environment for an array with parentheses. The cases environment puts a brace on the left and no delimiter on the right for mathematical case statements.
| Arrays of mathematics are typeset using one of the matrix environments as in \[\begin{bmatrix} 1 & x & 0 \\ 0 & 1 & -1 \end{bmatrix}\begin{bmatrix} 1 \\ y \\ 1 \end{bmatrix} =\begin{bmatrix} 1+xy \\ y-1 \end{bmatrix}. \] Case statements use cases: \[|x|=\begin{cases} x & \text{if }x\geq 0\,, \\ -x & \text{if }x< 0\,. \end{cases} \] Many arrays have lots of dots all over the place as in \[\begin{matrix} -2 & 1 & 0 & 0 & \cdots & 0 \\ 1 & -2 & 1 & 0 & \cdots & 0 \\ 0 & 1 & -2 & 1 & \cdots & 0 \\ 0 & 0 & 1 & -2 & \ddots & \vdots \\ \vdots & \vdots & \vdots & \ddots & \ddots & 1 \\ 0 & 0 & 0 & \cdots & 1 & -2 \end{matrix} \] |
Arrays of mathematics are typeset using
one of the matrix environments as in
\[
\begin{bmatrix}
1 & x & 0 \\
0 & 1 & -1
\end{bmatrix}\begin{bmatrix}
1 \\ y \\ 1
\end{bmatrix}
=\begin{bmatrix}
1+xy \\ y-1
\end{bmatrix}.
\]
Case statements use cases:
\[
|x|=\begin{cases}
x & \text{if }x\geq 0\,, \\
-x & \text{if }x< 0\,.
\end{cases}
\]
Many arrays have lots of dots all over
the place as in
\[
\begin{matrix}
-2 & 1 & 0 & 0 & \cdots & 0 \\
1 & -2 & 1 & 0 & \cdots & 0 \\
0 & 1 & -2 & 1 & \cdots & 0 \\
0 & 0 & 1 & -2 & \ddots & \vdots \\
\vdots & \vdots & \vdots & \ddots
& \ddots & 1 \\
0 & 0 & 0 & \cdots & 1 & -2
\end{matrix}
\]
|
LaTeX has a variety of ellipses:
- \cdots to type three dots horizontally (at the height of the centre of a + sign);
- \ldots to type three dots horizontally (at the height of a comma); use this outside of mathematics also, do not use '...' to typeset the three dots of an ellipsis;
- \vdots for three vertical dots; and
- \ddots for three diagonal dots.
Arrays embedded within arrays give more scope for your imagination. If a matrix environment is not quite flexible enough, then use the array environment which is the same as the tabular environment but for mathematics.
Equation arrays
Often we want to align related equations together, or to align each line of a multi-line derivation. The align mathematics environment does this. The align environment allows many columns: each column alternately right justified, left justified, and so on:
\begin{align}
... & ... & ... & ... \\
... & ... & ... & ... \\
... & ... & ... & ...
\end{align}
gives three rows, four columns, right-left-right-left
justified.
Beware: relational spacing, such as that around "=", is not done correctly if the relation is at the end of a right-justified cell! Instead organise so relations are at the start of a left-aligned cell.
Each line will be numbered by LaTeX, unless you specify \nonumber in a lines, or unless you use the * form of align. See Section 8 in Src/maths.tex.
| In the flow of a fluid film we may report \[\begin{aligned} u_\alpha & = \epsilon^2 \kappa_{xxx} \left( y-\frac{1}{2}y^2 \right), &(1) \\ v & = \epsilon^3 \kappa_{xxx} y\,, &(2) \\ p & = \epsilon \kappa_{xx}\,. &(3) \end{aligned}\] Alternatively, the curl of a vector field \((u,v,w)\) may be written with only one equation number: \[\begin{aligned} \omega_1 & = \frac{\partial w}{\partial y} -\frac{\partial v}{\partial z}\,, \\ \omega_2 & = \frac{\partial u}{\partial z} -\frac{\partial w}{\partial x}\,, &(4) \\ \omega_3 & = \frac{\partial v}{\partial x} -\frac{\partial u}{\partial y}\,. \end{aligned}\] Whereas a derivation may look like \[\begin{aligned} (p\wedge q)\vee(p\wedge\neg q) & = p\wedge(q\vee\neg q) \quad\text{by distributive law} \\ & = p\wedge T \quad\text{by excluded middle} \\ & = p \quad\text{by identity.} \end{aligned}\] |
In the flow of a fluid film we may report
\begin{align}
u_\alpha & = \epsilon^2 \kappa_{xxx}
\left( y-\frac{1}{2}y^2 \right),
\label{equ} \\
v & = \epsilon^3 \kappa_{xxx} y\,,
\label{eqv} \\
p & = \epsilon \kappa_{xx}\,.
\label{eqp}
\end{align}
Alternatively, the curl of a vector
field $(u,v,w)$ may be written with only
one equation number:
\begin{align}
\omega_1 & =
\frac{\partial w}{\partial y}
-\frac{\partial v}{\partial z}\,,
\nonumber \\
\omega_2 & =
\frac{\partial u}{\partial z}
-\frac{\partial w}{\partial x}\,,
\label{eqcurl} \\
\omega_3 & =
\frac{\partial v}{\partial x}
-\frac{\partial u}{\partial y}\,.
\nonumber
\end{align}
Whereas a derivation may look like
\begin{align*}
(p\wedge q)\vee(p\wedge\neg q)
& = p\wedge(q\vee\neg q)
\quad\text{by distributive law} \\
& = p\wedge T
\quad\text{by excluded middle} \\
& = p \quad\text{by identity.}
\end{align*}
|
Subequation numbering
Another useful facility of \usepackage{amsmath} is the subequations environment. It generates labels for the enclosed mathematics which are a base number followed by a,b,c,... in sequence, as illustrated below.
| \[\begin{aligned} u_\alpha & = \epsilon^2 \kappa_{xxx} \left( y-\frac{1}{2}y^2 \right), &(5a) \\ v & = \epsilon^3 \kappa_{xxx} y\,, &(5b) \\ p & = \epsilon \kappa_{xx}\,. &(5c) \end{aligned}\] Cross-reference to any individual equation, or to the collective (5). |
\begin{subequations}\label{eqf}
\begin{align}
u_\alpha & = \epsilon^2 \kappa_{xxx}
\left( y-\frac{1}{2}y^2 \right),
\label{equ} \\
v & = \epsilon^3 \kappa_{xxx} y\,,
\label{eqv} \\
p & = \epsilon \kappa_{xx}\,.
\label{eqp}
\end{align}
\end{subequations}
Cross-reference to any individual equation or to the
collective \cref{eqf}.
|
I once typeset a four line equation and discussed its physical relevance and implications in terms of the 'first line', 'second line', and so on. Unfortunately the journal's layout editor ruined my discussion by merging the four lines into two! I should have used subequations with labels for each of the four lines, and cross-referenced to the individual labelled lines.
Typesetting long expressions
Typesetting long multi-line expressions is an art normally too hard for computer recipes, so we usually code by hand in an align environment. Typically typeset line breaks in long expressions by inserting the code
\nonumber\\&\quad{}
Although if a delimiter is 'broken' across the line you
probably need to insert
\right.\nonumber\\&\left.\qquad{}
Insert either of the above on a line by itself in your
source code so that you can easily move the line break
around as needed.
Alternatively, if you need to be automatically flexible about multi-line presentation of long mathematical expressions, and you do not mind some crude typesetting, then perhaps invoke \parbox{}{} to help via the following command:
\newcommand{\parmath}[1]{\parbox[t]{0.8\linewidth}%
{\raggedright\linespread{1.4}\selectfont\(#1\)}}
\[
u_1=\parmath{ -2 \gamma \epsilon^{2} s_{2}+\mu \epsilon^{3}
... +\int_a^b 1-2x+3x^2-4x^3\,dx }
\]
Then the above expression is typeset like this:
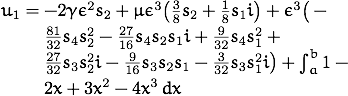
(The promising breqn package is not yet reliable enough for general use.)